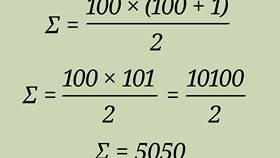Вероятность того, что сумма чисел будет кратна трём, зависит от условий задачи и выбранных чисел. Рассмотрим различные случаи и методы расчёта такой вероятности.
Содержание
Вероятность того, что сумма чисел будет кратна трём, зависит от условий задачи и выбранных чисел. Рассмотрим различные случаи и методы расчёта такой вероятности.
Случай двух случайных целых чисел
При выборе двух случайных целых чисел вероятность того, что их сумма делится на 3:
| Остатки при делении на 3 | Комбинации |
| 0 + 0 | Сумма кратна 3 |
| 1 + 2 | Сумма кратна 3 |
| Другие комбинации | Сумма не кратна 3 |
Вероятность: 3 благоприятных исхода из 9 возможных = 1/3 ≈ 33.33%
Сумма трёх случайных чисел
Для трёх случайных целых чисел вероятность кратности суммы трём:
- Все три числа имеют одинаковый остаток (0,0,0 или 1,1,1 или 2,2,2)
- По одному числу с каждым остатком (0,1,2)
- Вероятность: 7 благоприятных исходов из 27 = 7/27 ≈ 25.93%
Общий случай для n чисел
Для n независимых случайных целых чисел вероятность P(n) того, что их сумма делится на 3:
| Количество чисел (n) | Вероятность P(n) |
| 1 | 1/3 ≈ 33.33% |
| 2 | 1/3 ≈ 33.33% |
| 3 | 7/27 ≈ 25.93% |
| 4 | 20/81 ≈ 24.69% |
Специальные случаи
Сумма последовательных натуральных чисел
Для суммы первых n натуральных чисел S = n(n+1)/2:
- Кратность 3 зависит от остатка n при делении на 3
- Вероятность кратности стремится к 1/3 при n → ∞
Сумма чисел на игральных кубиках
Для суммы чисел на двух стандартных кубиках (2-12):
- Кратные 3: 3, 6, 9, 12
- Благоприятные исходы: 12 из 36
- Вероятность: 1/3 ≈ 33.33%
Заключение
Вероятность того, что сумма чисел кратна трём, в большинстве стандартных случаев стремится к 1/3. Точное значение зависит от конкретных условий задачи, количества слагаемых и способа их выбора. Для точных расчётов необходимо анализировать распределение остатков при делении на 3.
