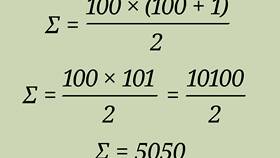Нахождение суммы целых чисел - фундаментальная математическая операция, используемая в различных вычислениях. Рассмотрим основные методы и правила сложения целых чисел.
Содержание
Основные правила сложения целых чисел
| Тип чисел | Правило сложения | Пример |
| Положительные + положительные | Складываем модули, результат положительный | 5 + 3 = 8 |
| Отрицательные + отрицательные | Складываем модули, результат отрицательный | -4 + (-2) = -6 |
| Положительные + отрицательные | Вычитаем из большего модуля меньший, знак как у большего | 7 + (-5) = 2 |
Методы нахождения суммы
Последовательное сложение
- Запишите все числа в ряд
- Складывайте по два числа слева направо
- Результат предыдущего сложения прибавьте к следующему числу
- Продолжайте до последнего числа
Попарное сложение
- Разбейте числа на пары
- Сложите числа в каждой паре
- Сложите полученные результаты
- Эффективно для большого количества чисел
Примеры вычислений
| Числа | Метод | Решение |
| 12, 8, 5, 7 | Последовательный | 12+8=20; 20+5=25; 25+7=32 |
| -3, 9, -2, 4 | Попарный | (-3+9)=6; (-2+4)=2; 6+2=8 |
Свойства сложения целых чисел
- Коммутативность: a + b = b + a
- Ассоциативность: (a + b) + c = a + (b + c)
- Существование нуля: a + 0 = a
- Существование противоположного: a + (-a) = 0
Особые случаи
| Случай | Решение |
| Сумма с нулем | Результат равен второму слагаемому |
| Сумма противоположных чисел | Всегда равна нулю |
| Большое количество слагаемых | Используйте группировку удобных чисел |
Практические советы
- Для отрицательных чисел заключайте в скобки
- Сначала сложите все положительные числа
- Затем сложите все отрицательные числа
- Сложите полученные результаты
- Проверьте вычисления обратным действием
Овладение техникой сложения целых чисел позволяет быстро и точно выполнять различные математические операции и решать практические задачи.