Сумма углов треугольника - это фундаментальное свойство евклидовой геометрии, которое изучается в школьном курсе математики. Данная теорема имеет важное значение для понимания свойств геометрических фигур.
Содержание
Сумма углов треугольника - это фундаментальное свойство евклидовой геометрии, которое изучается в школьном курсе математики. Данная теорема имеет важное значение для понимания свойств геометрических фигур.
Основная теорема о сумме углов
В евклидовой геометрии сумма внутренних углов любого треугольника всегда равна 180 градусам. Это утверждение справедливо для всех типов треугольников: остроугольных, прямоугольных и тупоугольных.
Доказательство теоремы
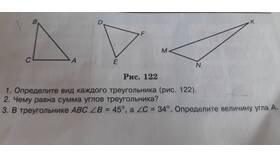
Рассмотрим произвольный треугольник ABC:
- Проведем через вершину B прямую, параллельную стороне AC
- Образовавшиеся углы при точке B составят развернутый угол (180°)
- Эти углы равны соответствующим углам треугольника как накрест лежащие
- Следовательно, сумма углов A, B и C равна 180°
Примеры для разных типов треугольников
| Тип треугольника | Пример углов | Сумма |
| Остроугольный | 60°, 60°, 60° | 180° |
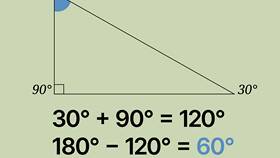
| Прямоугольный | 90°, 45°, 45° | 180° |
| Тупоугольный | 100°, 40°, 40° | 180° |
Исключения в неевклидовой геометрии
В геометрии Лобачевского (гиперболической геометрии) сумма углов треугольника всегда меньше 180 градусов. В эллиптической геометрии (на сфере) сумма углов треугольника всегда больше 180 градусов.
Практическое применение
- Расчет неизвестных углов в геометрических задачах
- Построение чертежей и технических схем
- Определение формы земельных участков
- Решение задач навигации и картографии
